This problem can be solved by transforming the volume to an intermediate coordinate system for which there is a very simple mapping from the object coordinate system. Affine transformations are transformations that map parallel lines into parallel lines. The decomposition of an affine transformation has a simple geometric interpretation: The result is a sequence of shears in different directions.
In the volume, each voxel is represented as v($x_n$, $y_n$, $z_n$), with the coordinates ($x_n$, $y_n$, $z_n$) determining the location. Assume that in the beginning, the z axis of the volume is aligned to the ray. Each 2D slice S($x_n$, $y_n$) is directly mapped onto one of the 64x128 MPP processor arrays. Volume data is then addressed in the processor array according to its x and y coordinates. All data referenced by the same ray are assigned the same x and y pair, on the same processor. The pixel color rendered by the ray $R_{(x,y)}$ is: \[C_{R_{(x,y)}} = \sum_{z_n} w_{z_n} v(x_n, y_n, z_n ) \]
After rotation, the direct coordinate transformation obtains new coordinates by matrix transformation: \[ (x_n^{new}, y_n^{new}, z_n^{new}) = (x_n, y_n, z_n) \times M_{tran} \]
Generally, the voxels with the same $x_n^{new}$, $y_n^{new}$ are distributed across many processors. Because the direction and distance to transport each voxel to destination processor are different, the number of active processors on the MPP is very small during communicating. In order to gather all voxels visited by the same ray on the same processor, O($n^3$) inter-processor communication operations are necessary on the MPP. Loss of parallelism and high communication cost currently make real-time rendering of this order impossible.
Based on the three-pass affine transforms method, a shear-warp algorithm is used to factor the viewing transformation into a 3D shear and a 2D warp transformations. \[ (x_n^{new}, y_n^{new}, z_n^{new}) = (x_n, y_n, z_n) \times M_{tran} = (x_n, y_n, z_n) \times M_{shear} \times M_{warp}\] In the shearing coordinate system, each 2D slice maps to the same vertical position but shifts relative to the previous one. The z axis of the shearing volume is always aligned to the ray. After shearing, each processor owns all voxels to be composited along a ray. \[ (x_n^{shear}, y_n^{shear}, z_n^{shear}) = (x_n, y_n, z_n) \times M_{shear} = ((x_n-z_n/a), (y_n-z_n/b), z_n) \]
Because all voxels in a 2D slice shift to the same direction and same distance during shearing, all processors in the array could execute the same transformation instruction %`xnet*[distance]' (*: direction) concurrently. In this step, all processors are active and only O(n) communication operations are needed to shear $n^3$ volume.
A 2D warp to form an undistorted final image requires O($n^2$) communication operations by direct warp technique. Once again, a multi-pass transformation technique is applied to decompose the 2D warping transformation into two 1D x-pass and y-pass transformations, each of which could be implemented by executing O(n) communication operations on MPP. For each communication operation, the processors in 2D array are active only in 1D.
In conclusion, overall O(n) communication operations are necessary to obtain an final rendered image by the shear-warp algorithm on MPP. Compared to the O($n^3$) operations introduced by direct coordinate transformation, the shear-warp algorithm has resulted in a satisfactory frame-rate. % only by eliminating communication contention. During informal experiments, the MPP parallel machine was used to render one image in about 0.6-0.8 second. When the serial images rendered from consecutive viewing directions are consecutively displayed in a short time (about 3-5 frames/second), the main interior structure in the `rotating' or `rocking' volume was easily identified. It is unambiguous that recovering 3D structure from motion was successful in our experiment.
Animated gifs for the rocking effects
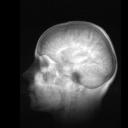
|
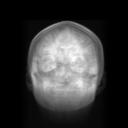
|
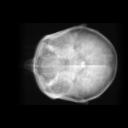
|
Side - | Front - | Up - |
